Find the 8th term of the geometric sequence – In the realm of mathematics, geometric sequences hold a significant place. Embark on a journey to unravel the intricacies of geometric sequences and master the art of finding their 8th term. This comprehensive guide will provide you with a deep understanding of this fundamental concept, empowering you to solve complex problems with precision and confidence.
Geometric sequences, characterized by a constant ratio between successive terms, are ubiquitous in various fields, from finance to physics. Understanding how to find the 8th term of a geometric sequence is crucial for solving a wide range of problems.
Finding the 8th Term of a Geometric Sequence: Find The 8th Term Of The Geometric Sequence

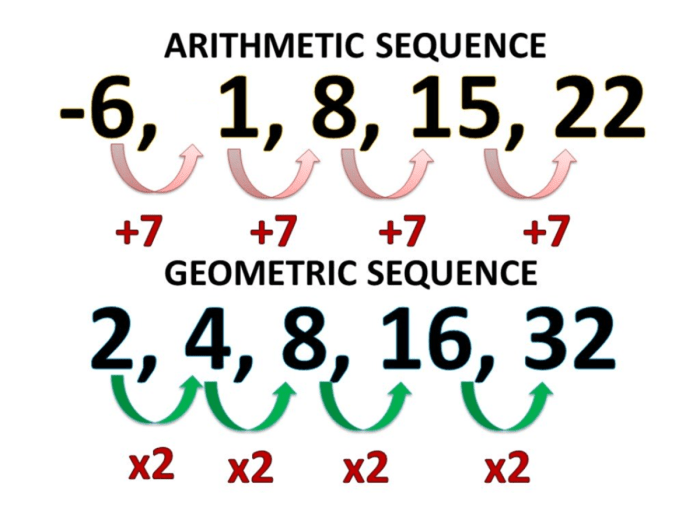
A geometric sequence is a sequence of numbers where each term after the first is found by multiplying the previous term by a constant value, known as the common ratio. For example, the sequence 2, 4, 8, 16, 32, … is a geometric sequence with a common ratio of 2.
The nth term of a geometric sequence is given by the formula:
an= a 1
r(n-1)
where:
- a nis the nth term of the sequence
- a 1is the first term of the sequence
- r is the common ratio
- n is the term number
Finding the 8th Term, Find the 8th term of the geometric sequence
To find the 8th term of a geometric sequence, simply substitute n = 8 into the formula:
a8= a 1
r(8-1)
For example, if the first term of the sequence is 2 and the common ratio is 3, the 8th term would be:
a8= 2
- 3 (8-1)= 2
- 3 7= 2
- 2187 = 4374
Example Problem
Find the 8th term of the geometric sequence 5, 10, 20, 40, …
Solution:
The first term of the sequence is a 1= 5 and the common ratio is r = 2. Substituting these values into the formula, we get:
a8= 5
- 2 (8-1)= 5
- 2 7= 5
- 128 = 640
Therefore, the 8th term of the sequence is 640.
Applications
Finding the 8th term of a geometric sequence has applications in various fields, including:
- Finance: Calculating the future value of an investment or the present value of a future cash flow
- Physics: Determining the distance traveled by an object in free fall
- Biology: Modeling population growth or decay
Helpful Answers
What is the formula for finding the nth term of a geometric sequence?
nth term = a – r^(n-1), where ‘a’ is the first term, ‘r’ is the common ratio, and ‘n’ is the term number.
How do I find the 8th term of a geometric sequence?
Use the formula nth term = a – r^(n-1), where ‘a’ is the first term, ‘r’ is the common ratio, and ‘n’ is 8.
What are some real-world applications of geometric sequences?
Geometric sequences find applications in population growth, radioactive decay, compound interest, and many other areas.