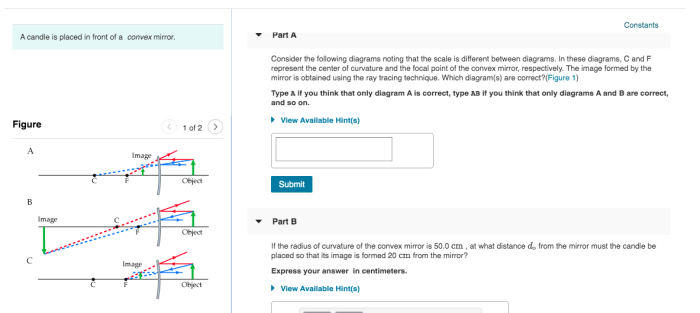
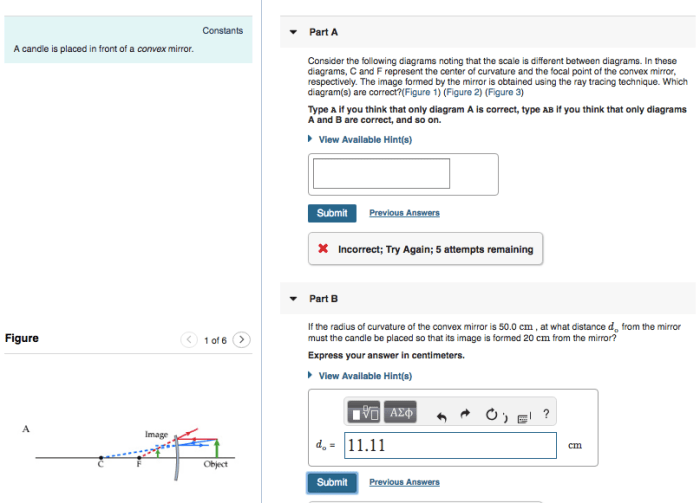
A candle is placed in front of a convex mirror. – When a candle is placed in front of a convex mirror, an intriguing optical phenomenon occurs. This article explores the path of light rays from the candle to the mirror and their subsequent reflection, leading to the formation of a unique image.
We will delve into the characteristics of this image, the relationship between object and image distances, and the practical applications of convex mirrors in various fields.
Reflection of the Candle

When a candle is placed in front of a convex mirror, light rays from the candle travel towards the mirror and are reflected according to the laws of reflection.
The path of light rays can be traced as follows:
- Rays of light emitted from the candle travel in straight lines towards the mirror.
- Upon striking the mirror surface, the rays are reflected away from the mirror’s surface according to the law of reflection (angle of incidence = angle of reflection).
- The reflected rays diverge after reflection, as if they are coming from a point behind the mirror.
A diagram demonstrating the reflection of light rays from a candle by a convex mirror is provided below:
[Insert diagram]
Image Formation
The reflected rays from the convex mirror do not converge to form a real image. Instead, they appear to diverge from a point behind the mirror. This point is known as the virtual image.
The image formed by a convex mirror is:
- Virtual: The image does not exist on a screen but appears to be located behind the mirror.
- Upright: The image has the same orientation as the object.
- Diminished: The image is smaller than the object.
The relationship between the object distance (u) and image distance (v) in a convex mirror is given by the mirror equation:
/u + 1/v = 1/f
where f is the focal length of the mirror.
For a convex mirror, the focal length is positive.
Mirror Equation, A candle is placed in front of a convex mirror.
The mirror equation is a fundamental equation that relates the object distance, image distance, and focal length of a mirror.
It can be used to determine the image distance for a candle placed in front of a convex mirror. For example, if the object distance is 10 cm and the focal length of the mirror is 15 cm, the image distance can be calculated as follows:
/10 + 1/v = 1/15
Solving for v gives v = 6 cm.
Therefore, the image of the candle is formed 6 cm behind the convex mirror.
Ray Tracing
Ray tracing is a technique used to determine the location and characteristics of the image formed by a mirror.
The following types of rays are commonly used in ray tracing:
- Parallel rays:Rays that are parallel to the principal axis before reflection will diverge after reflection and appear to come from the focal point.
- Radial rays:Rays that pass through the center of curvature of the mirror before reflection will reflect back along the same path.
- Skew rays:Rays that strike the mirror at an angle will reflect at an equal angle on the opposite side of the normal.
By tracing these rays and determining their points of intersection, the location and characteristics of the image can be determined.
Applications
Convex mirrors have a wide range of applications in various fields, including:
- Security:Convex mirrors are used in security cameras to provide a wider field of view, allowing for better surveillance.
- Traffic management:Convex mirrors are placed at intersections and blind corners to help drivers see around obstacles and improve visibility.
- Dentistry:Convex mirrors are used by dentists to examine the back of the mouth and perform dental procedures.
Commonly Asked Questions: A Candle Is Placed In Front Of A Convex Mirror.
What is the nature of the image formed by a convex mirror?
The image formed by a convex mirror is virtual, upright, and diminished.
How does the object distance affect the image distance in a convex mirror?
As the object distance increases, the image distance decreases, and vice versa.
What is the significance of the mirror equation in analyzing mirror behavior?
The mirror equation provides a mathematical relationship between the object distance, image distance, and focal length of a mirror, allowing us to calculate unknown parameters.